T · Asíntotas
Estudiamos la función cuando `x->+oo`
1º.- Calculamos `lim_(x->+oo)f(x)`
a) Si `lim_(x->+oo)f(x)=k =>` la recta `y=k` es AH (asíntota horizontal)
b) Si `lim_(x->+oo)f(x)=oo =>` no hay AH, vamos al paso 2º
2º.- Calculamos `m=lim_(x->+oo) f(x)/x` y `n=lim_(x->+oo) (f(x)-mx)`
a) Si `m="finito" !=0` y `n "es finito" =>` la recta `y=mx+n` es AO (asíntota oblicua)
b) Si `m=oo =>` RP (rama parabólica) en la dirección del eje de ordenadas
c) Si `m=0 =>` RP (rama parabólica) en la dirección del eje de abscisas
3º.- Para analizar el comportamiento de `f` cuando `x->-oo` se repite el proceso, pero esta vez tomando límites cuando `x->-oo` (además, debemos tener en cuenta que no tiene porqué suceder lo mismo que cuando `x->+oo` , aunque a veces ocurra)
Ejemplos:
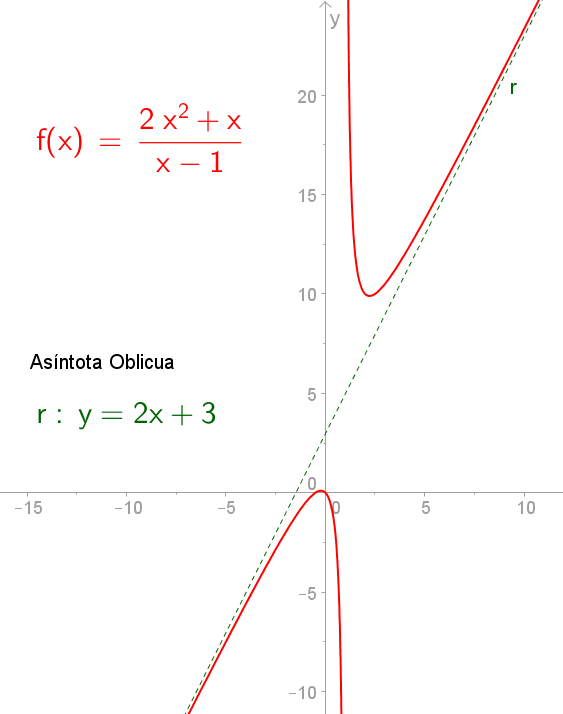
[ Cálculo ]