
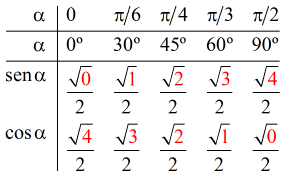
Podemos recordar fácilmente el valor de las razones trigonométricas seno y coseno de los ángulos básicos si los escribimos de esta forma:
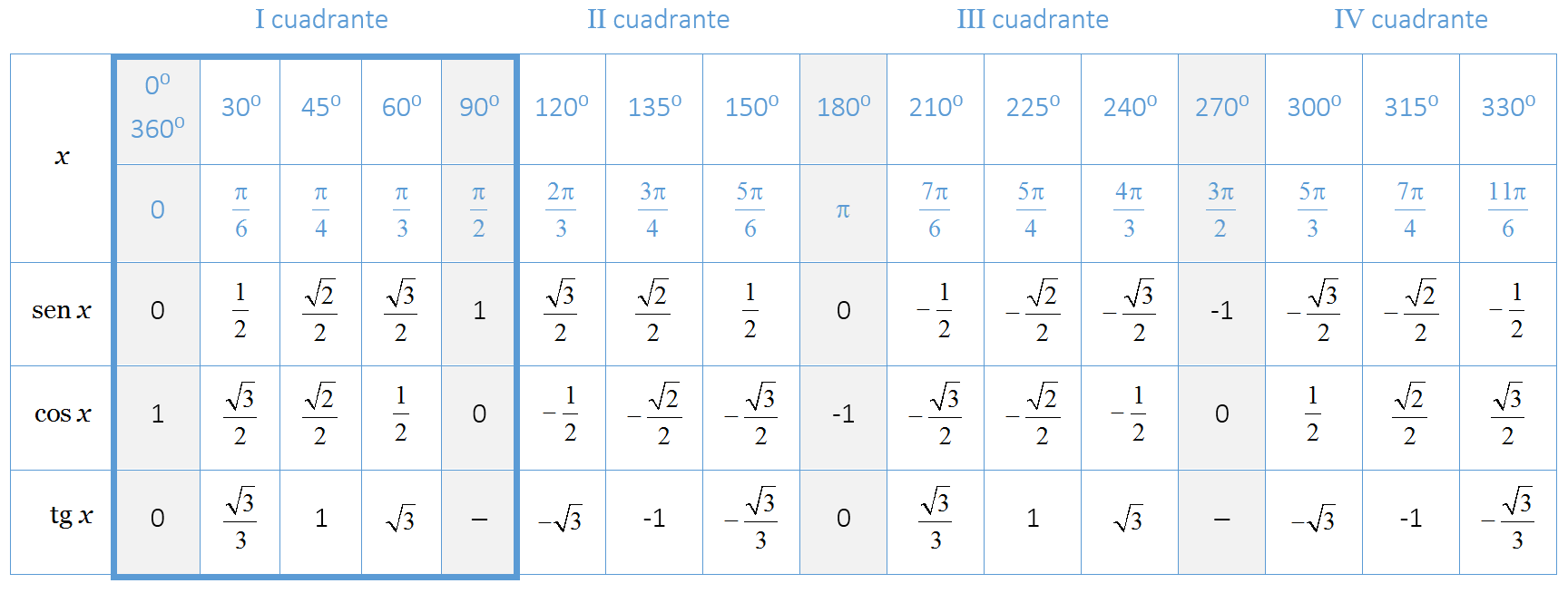
En la siguiente tabla se dan los valores del seno, coseno y tangente para los principales ángulos medidos en grados `[0º,360º]` y en radianes `[0,2pi]`. Para otros ángulos se utilizará la calculadora.
[ Trigonometría ]
Problema r004
Calcula la longitud de una tabla de madera apoyada sobre un bloque (ortoedro) de 5 m de altura, sabiendo que el ángulo formado con la horizontal es de 63,43º.
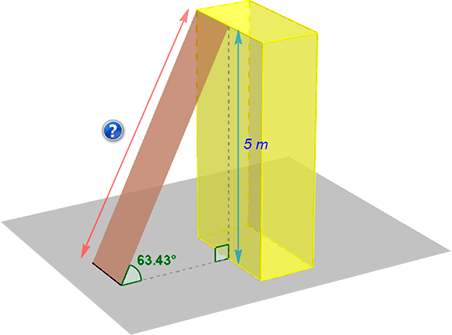
`sen 63,43º = 5/t`
`t=5/{sen 63,43º}~~5,6 m`
Hoy ........ 386
Ayer ....... 1798
Mes ....... 46676
TOTAL ... 5614228
Hay 56 invitados y ningún miembro en línea