A · Números Irracionales [Guía]
El concepto "número irracional" viene de la Escuela Pitagórica (s. VI a.C.) , que descubrió la existencia un tipo de números que no eran enteros ni tampoco se podían expresar como fracciones.
- Los números irracionales no se pueden expresar como el cociente de dos números enteros.
- Los números irracionales son números que tienen infinitas cifras decimales no periódicas.
Sabemos que el conjunto de los números reales, `RR`, está formado por los números racionales, `QQ`, más los números irracionales, es decir:
`RR = ` Racionales + Irracionales, luego los irracionales se pueden expresar como: `RR - QQ`
Los números reales pueden subdividirse en conjuntos según muchos criterios de clasificación.
Los números algebraicos son los números reales que son solución de alguna ecuación polinómica cuyos coeficientes son números racionales. A la vista de esta definición es fácil comprender que todos los números racionales son algebraicos. Pero no sólo son algebraicos los números racionales, también lo son muchos irracionales.
Por ejemplo, el número irracional `sqrt(2)` es algebraico. Y también lo es el número áureo `phi` cuyo valor, como sabemos, es `{1+sqrt(5)}/2`.
Los números trascendentes son los números reales que no son solución de ninguna ecuación polinómica de coeficientes racionales. Por lo que hemos visto antes todos los números trascendentes son irracionales, aunque no todos los irracionales son trascendentes.
Como ejemplos más representativos de números irracionales transcendentes tenemos al número `pi` y al número `e`.
Resumiendo:
- Irracionales Algebraicos son aquellos irracionales que surgen de resolver algún tipo de ecuación algebraica, escribiéndose con un número finito de radicales libres o anidados (en general, las raices no exactas de cualquier orden).
- Irracioneales Trascendentes son aquellos que no pueden ser representados a través de un número finito de radicales libres o anidados, sino que provienen normalmente de operaciones con funciones trascendentes (logarítmicas, trigonométricas, exponenciales, etc). Los irracionales transcendentes también pueden surgir de la simple acción de escribir números decimales al azar sin periodicidad y sin un patrón determinado.
Algunos números irracionales:
El número pi, `pi`
Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. Es la relación entre la longitud de una circunferencia y su diámetro.
El valor numérico de π, truncado a sus primeras cifras, es
`pi = L/{2r} ; pi = 3,1415926535...`
El valor de `pi` se ha obtenido con diversas aproximaciones a lo largo de la historia.
- Antiguo Egipto (1800 a.C.): `pi ~= 256/81=3,16`
- Mesopotamia (1900-1600 a.C.): `pi~=25/8=3,125`
- Antigüedad clásica, Ptolomeo (s.II): `pi~=377/120=3,1416...`
- China: (s. I) `pi~=142/45=3,15...` ;
(s. V) `pi~=22/7=3,142857...` ; `pi~=355/113=3,14159292...`
El número phi, `phi`
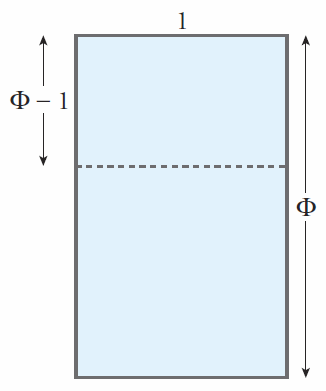
También llamado número áureo. Se trata de un número algebraico irracional, descubierto antiguamente y con numerosas propiedades interesantes.
En la imagen se representa el rectángulo áureo.
`phi = {1+sqrt(5)}/2~~1,6180339887...`
El número `e`
Es uno de los más importantes números reales irracionales y trascendente. Los logaritmos neperianos tienen como base el número e. Juega un papel muy importante en el cálculo y análisis matemático.
`e = 2.71828182845904...`
Una de las formas de obtenerlo es mediante el cálculo del límite de la sucesión que tiene como término general: `a_n=(1+1/n)^n` cuando `n` tiende a `oo`, es decir: `lim_(x->oo) (1+1/n)^n=e`
La raíz de dos, `sqrt {2}`
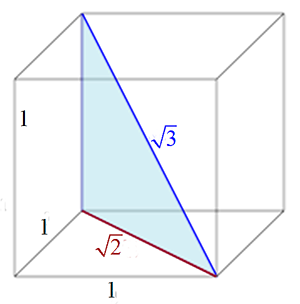
La raíz de 2, que la encontramos al intentar calcular la diagonal de un cuadrado de lado 1 unidad, utilizando el teorema de Pitágoras.
`sqrt{2} = 1,41421356237309...`
La raíz de tres, `sqrt {3}`
La raíz de 3, del mismo modo a la anterior, la encontramos al calcular la diagonal de un hexaedro o cubo, cuyas aristas son todas iguales a 1 unidad.
`sqrt{3} = 1,73205080756887...`